サイクルロードレースでは、いかに空気抵抗を減らして、体力を温存できるかが、勝敗を分ける鍵になる。
チーム戦術として、1番勝てそうな選手の体力を温存するために、犠牲になって風除けになる、アシストという役割の選手もいる。
そこから、推測すると、イワシの大群も多分体力を温存するために、あのような一糸乱れぬ同期した動きをしているのだと思う。
前を泳ぐイワシから一定の距離を保つことによって、水の抵抗を最小限にとどることができるはず。
また、映像を見ると、イワシの群れは、円運動を行なっているため、直進する自転車のロードレースのような空気抵抗を受ける先頭すらなくなっている。
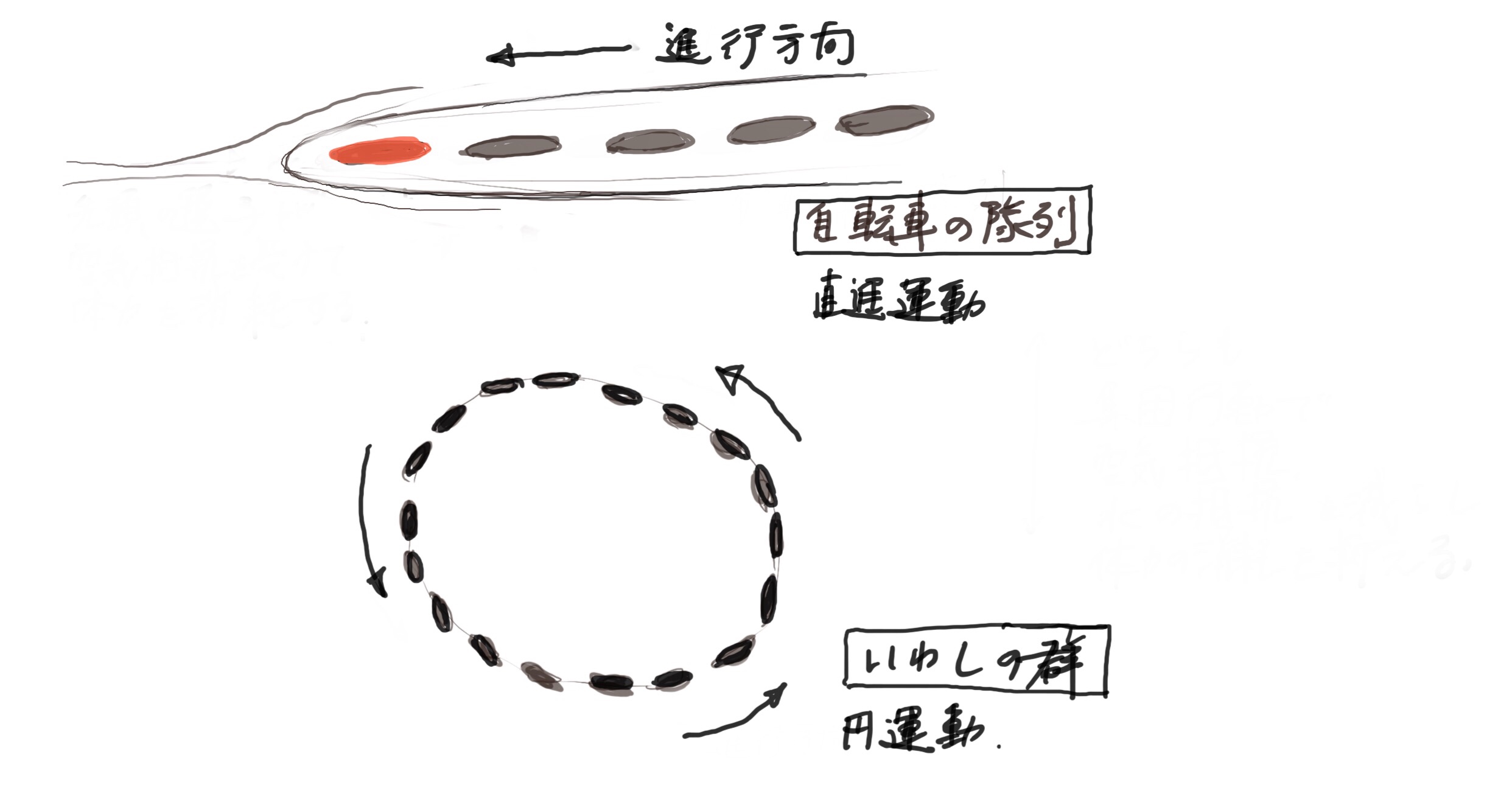
自転車に関する理論は、かなり錯綜しているように感じる。
(物理学の基本を無視したのものがほとんど。)
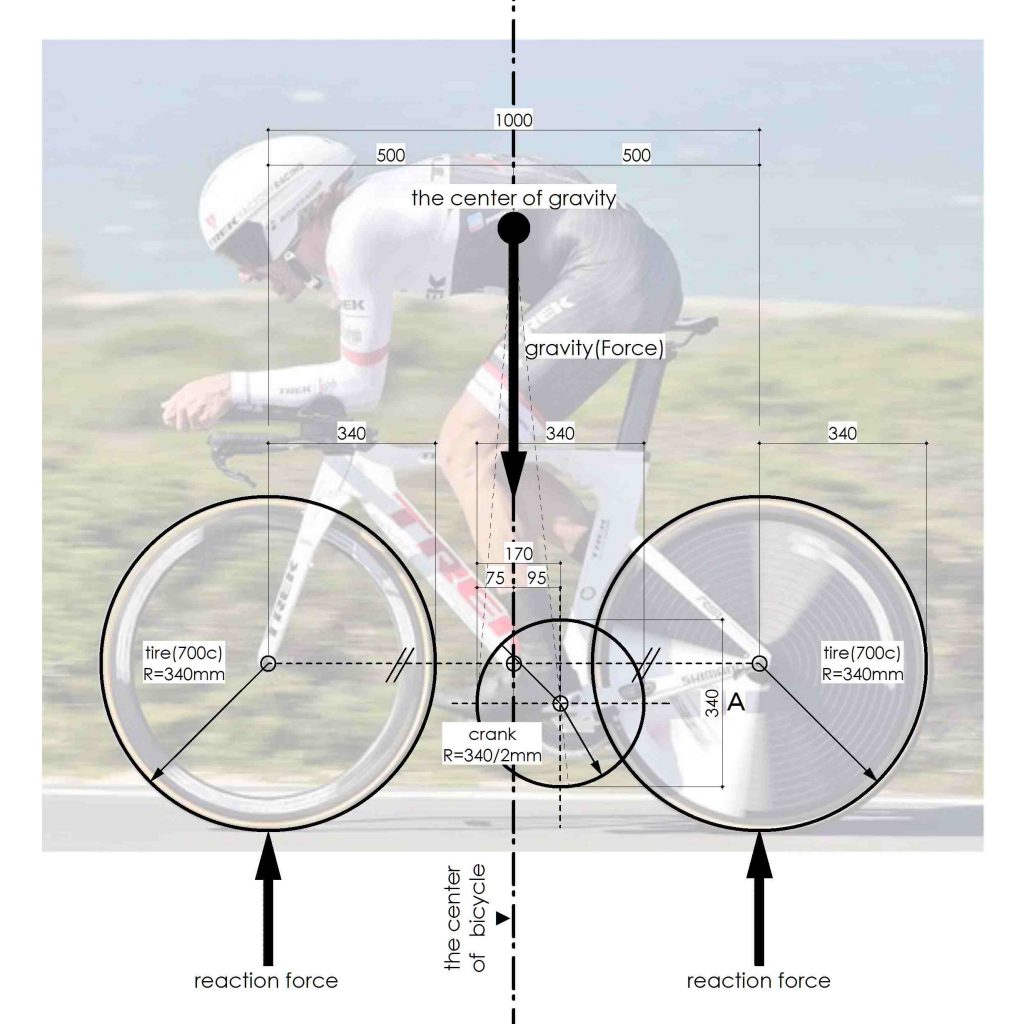
そこで、改めて自転車が進む力を物理学的に図式化してみたのが上図である。
ライダーの体重は、ハンドルとサドル、そしてペダルの三点で支えられる。
そして、ペダルで支える体重が、ペダルを回し、自転車を推進させる力になる。
鉛直方向への仕事量は、ペダルにかかる体重の位置エネルギーに等しいから、質量と鉛直方向への移動距離(つまり、クランクの直径)と重力加速度との積になる。
また、速度を上げるためには、時間当たりの仕事量＝仕事率W（ワット）を増やせばいい。
仕事率は、仕事量と毎秒の回転数の積として、以下の式で表される。
仕事率(W)=Mp(kg) • 0.34(m) • 2 •G(N/kg) • n (/sec)
この式から、ペダルにかかる体重かケイデンスを上げることができれば、仕事率が大きくなり、速度も上がる。
この図式に基づけば、セッティングやペダリングを合理的に考える事ができる。
例えば、ペダルを回すのに、重いギアでゆっくりか、軽いギアで速くか、どちらが優れているか、という議論がある。
これは上記の図式から考えれば、答えは明らかである。
先に記した通り、仕事率は単位時間あたりの加えられる力と距離の積であり、ギア比は、仕事率に直接関係しない。
よって、ペダルに同じ力がかけられるのであれば、速く回した方が、大きな仕事量を得ることができる。ただ、軽いペダルに十分な体重を載せることが、技術的に難しいだけである。
Read more »
自転車に働く力と幾何学。
２つのタイヤが地面から受ける反力は、自転車とそれに乗る荷重(人の体重など)の合計に等しく、一定である。
自転車の推進力もこの閉じた力の系の中からしか生まれない。